Итак, продолжим анализ значений раздела статистики известного как гистограмма. В прошлой части мы обсудили все колонки этого раздела на примере резалт-сета полученного для нашей тестовой таблицы. Однако, отдельного анализа заслуживает и первая строка все того же резалт-сета, содержащая самое первое (наименьшее; или, по графику — самое левое) опорное значение, 'A_0', в нашем случае. Во-первых, такая опорная точка всегда имеет минимальное значение колонки. Все вычисления, все значения в колонках обсуждаемого резалт-сета, базируются на шагах гистограммы, как мы знаем. Первый шаг должен начинаться с первого же значения. Поэтому минимальное значение в колонке для которой строится гистограмма всегда и без вариантов назначается первым опорным значением. Во-вторых:
- RANGE_ROWS — будет всегда 0. У нас еще не сформирован первый шаг и мы не можем говорить о диапазоне.
- EQ_ROWS — количество строк с этим самым минимальным опорным значением. Тут все как обычно, для этой цифры диапазон значений не требуется.
- DISTINCT_RANGE_ROWS — будет всегда 0 по тем же причинам что и в RANGE_ROWS.
- AVG_RANGE_ROWS — будет всегда 1. Как «грамотно» делить 0 на 0 мы обсудили в конце предыдущей, 4-й части статьи.
Таким образом, для самого первого опорного значения единственная валидная колонка — EQ_ROWS. Остальные колонки содержат сугубо формальные цифры.
Как увидеть важность параметра Selectivity?
Ну этот-то как раз не сложнее той же процедуры с предыдущим параметром, плотностью. Снова, в отдельной вкладке редактора, напишите какой-нибудь запрос к нашей тест-таблице с предикатом, допустим такой подойдет:
1 | SELECT * FROM TT WHERE X='A_15' |
Снова вызовите предполагаемый план исполнения и в шаге Table Scan посмотрите на все те же Estimated Number of Rows. Убедитесь, что он совершенно корректен — 10. Именно столько строк в нашей таблице имеют указанное значение. Предвижу ваш вопрос —«а стоило ли заморачиваться с селективностью? Кажется, что и плотность здесь будет вполне себе в порядке?». Проверим это предположение. Какова плотность колонки X в новой редакции таблицы TT? У нас 1000 уникальных значений, так что D(X)=1/1000=0.001. Можете в этом легко убедиться командой DBCC SHOW_STATISTICS с параметром DENSITY_VECTOR. А тогда — как с привлечением плотности посчитать число строк ожидаемых на выходе последнего запроса? Да, мы это уже «проходили», это среднее количество дубликатов в таблице и расчет его: AVG_DBL(X)=0.001*10'000=10. Действительно, все сошлось. НО! Ведь строк с 'A_15' могло быть и не 10! А одна. Или пару сотен. Расчеты этого абзаца не изменились бы ни на йоту (проверьте!), и движок сервера считал бы что он получит «где-то, примерно» 10 строк. Одним словом — мы все это уже обсудили: как только у нас в колонке «перекос данных», плотность тут же «сливает по полной». Вот что бы хоть как-то нивелировать эффект такого перекоса цифра 10 выше была получена совсем не из значения плотности, а и из значения гистограммы. Хотите в этом убедиться? Не проблема.
Возьмите строчку кода добавляющего в нашу таблицу еще значений 'A_15':
1 | insert into TT values ('A_15') |
и «клонируйте» ее так, что бы после исполнения получившегося пакета инструкций число строк с 'A_15' стало ощутимо больше 10-ти. Допустим, ваш пакет будет состоять из 15-ти таких инструкций, а после его исполнения число строк со значением 'A_15' станет 10+15=25. Теперь, поскольку число одной их опорных точек возрасло более чем в 2 раза статистику нужно перестроить, иначе мы не увидим эффекта:
1 | UPDATE STATISTICS TT(X) |
А помимо этого, нужно еще очистить кэш планов, как мы проделывали это в упражнениях по многоколоночной плотности. Причины заставляющие нас сделать эту процедуру ровно те же самые, что были описаны в параграфе по приведенной ссылке. Наконец, вернитесь на вкладку с командой
1 | SELECT * FROM TT WHERE X='A_15' |
и обновите план выполнения самой этой команды. Однако, помните, саму команду исполнять не нужно. Мы же пытаемся выяснить какой из оптимизатора «Нострадамус» в плане предсказаний будущих событий или, как минимум, будущих цифр. Смотрим — что у нас теперь в плане?
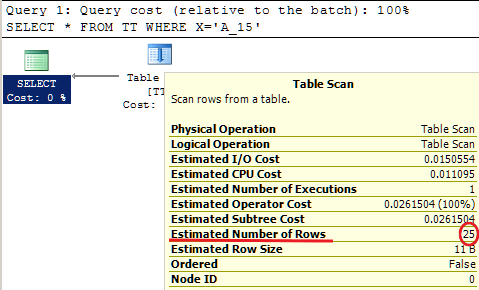
Идеальное предсказание! Отметьте себе, что, как мы и говорили ранее, все наши действия нисколько не отразились на величине плотности, как она была 0.001, так и осталась. Так что отмеченное на последней иллюстрации значение определенно получено из гистограммы. Но вот как? Посмотрим как выглядит обновленная статистика в разрезе гистограммы для таблицы с 25-ю значениями 'A_15'. Снова первые 5 строк:
A_0 0 10 0 1
A_15 60 25 6 10
A_19 30 10 3 10
A_22 30 10 3 10
A_26 30 10 3 10
Изменения минимальнейшие, а точнее одно: число строк с опорным значением 'A_15' стало 25 вместо 10. Собственно, вот эти 25 и 25 с последней иллюстрации есть одно и тоже число. При анализе нашего запроса оптимизатор обнаружил, что значение предиката совпадает с одним из опорных значений. А значит, рассудил он, можно взять число из колонки EQ_ROWS этого значения да и делу конец. Что ж — логично. Ну а отсюда рукой подать до вычисления совершенно корректного значения селективности: S(X,'A_15')=25/10000=0.0025. А обладание точной селективностью (наряду со знанием о точной плотности) — ключ к выбору оптимизатором наиболее эффективного плана исполнения, о чем речь пойдет в следующей и заключительной части статьи.
А что если в предикате будет не опорное значение? Тогда будет найден тот шаг гистограммы в которое это значение «укладывается» и взята цифра колонки AVG_RANGE_ROWS этого шага. Для предиката ...WHERE X='A_24' в последнем резалт-сете будет найдена строчка с A_22 A_26 (т.к. A_24 принадлежит шагу начинающемуся заканчивающемуся этим опорным значением; спасибо читателю блога Victor Pozhitkov за уточнение этого момента — промежуточные значение опираются на большее, а не меньшее, опорное значение. Т.е. на ближайшее опорное, но непременно большее) и взято значение из упомянутой колонки этой строки — 10. Как мы и говорили, движок считает что в пределах каждого шага число любых промежуточных значений одинаково и равно их усредненному значению. Неизбежная плата за сжатие информации — потеря ее точности, увы.
Все становится еще интересней, если у предиката указать значение не существующее в таблице. Допустим, размер колонки X не 4 символа как у нас, а 7. Данные же абсолютно те же что и сейчас, а предикат имеет вид ...WHERE X='A_24abc'. Готовы самостоятельно объяснить, как в таком случае оптимизатор будет искать предполагаемое число строк и выводить из нее значение селективности? Самое интересное, что и объяснять ничего не придется, это уже сделано в предыдущем параграфе! Да, обработка значений 'A_24' и 'A_24abc' абсолютно идентична, просто потому, что они «укладываются» в один и тот же шаг гистограммы. И — да, хоть и увы — оптимизатор сделает совершенно неправильный вывод о предполагаемом количестве строк прошедших через такой предикат. Он будет ориентироваться на 10 строк и выдаст ориентировочную селективность S(X,'A_24abc')=10/10000=0.001, в то время как правильный расчет селективности был бы S(X,'A_24abc')=0/10000=0. Баг ли это? Совершенно точно нет. Это поведение «by design» и, опять же, лишь отражение того факта, что статистика содержит усредненную, весьма далекую от идеала, можно сказать обзорную информацию по значениям колонки. Зато она весьма лаконична и ее обновление не вызывает ступор всей системы на секунд 20. Да, да, вы правы — этот мир состоит из компромиссов...
Что если колонок больше одной?
Мы задавали тот же самый вопрос при изучении плотности и он привел нас к необходимости понимания отдельного процесса: как создается и используется «плотность в сочетании». А что в случае селективности? Еще одна большая тема? К сожалению (или счастью, кому как) никакой темы не будет. При создании статистики по сочетанию столбцов гистограмма строится лишь для значений самого левого из них. И, таким образом, полностью эквивалентна гистограмме построенной персонально для этого столбца. Точка, end of story.
Селективность и индексы.
Да, я знаю что это статья не о индексах! И более того — я категорически не хочу разворачивать ее в этом направлении и начинать обсуждать эту большую и даже огромную тему, текущий объем материала и так уже «зашкаливает». Соблазн велик, поскольку индексы — ничто без статистики. Недаром же при создании нового индекса он получает последнюю «в подарок», даже делать для этого ничего не надо. Однако — нет и нет, оставим индексы на следующий раз, тем более статья по одной из их разновидностей уже почти готова, как говорится — следите за обновлениями на блоге. ![]()
Ну а цель этого совсем маленького раздельчика — упомянуть (вообще без технических деталей и нюансов) об одной очень важной точке в которой «сходятся» индексы (и кластерные, и нет) и как раз селективность. Вы, несомненно, слышали или читали на форумах вопрос вида: «у меня на таблице есть индекс и запрос, которому этот индекс подходит идеально, однако согласно плану исполнения индекс не используется — почему?». В тех рамках и объемах которые мы обозначили как допустимые для этого почти побочного вопроса ответ будет крайне прост: потому что ему не хватает селективности! Опять же, вспомните предупреждение в начале предыдущей части и лишний раз обратите внимание, что обычно когда говорят/пишут «не хватает селективности» имеют в виду малую избирательность, но значение селективности в такой ситуации как раз будет высоким. Так вот, для индекса ведется абсолютно та же самая статистика с которой мы с вами работали на протяжении всей статьи. И оптимизатор при оценке [не]нужности использования индекса для данного запроса смотрит прежде всего именно на нее, на селективность. Чем более избирателен индекс, тем больше шансов на его включение в план. При превышении значения селективности индекса некоторого порога, т.е. при его «движении» в сторону единицы, индекс вообще перестает рассматриваться как альтернатива и применяются иные шаги-операторы плана исполнения, в основном полное сканирование таблицы. Конкретного числового значения этого «некоторого порога» касаться не будем, это опять тема отдельной заметки, тут снова отнюдь не все так однозначно как хотелось бы и оптимизатор подчас бывает на удивление «гибок» в принятии решений. Ограничимся констатацией факта: такой порог есть и его наличие — ответ на популярный вопрос приведенный выше.
Все ли я правильно понял о селективности?
Не сомневаюсь что да, но лучше в этом снова убедиться самому.
1. Какое минимальное и максимальное значение может принять параметр селективности для данной колонки и данного предиката?
2. При прочих равных, больше строк в итоговом резалт-сете мы получим от предиката селективностью 0.05 или селективностью 0.00002?
3. В каком разделе статистики хранятся данные на основе которых оптимизатор легко и довольно точно вычисляет значения селективностей колонок?
4. Способен ли оптимизатор совершенно точно рассчитать для любой колонки и любого предиката значение селективности?
5. Мы знаем селективность данного предиката S и общее количество строк в таблице T. Привести формулу для расчета N, где N — предполагаемое число строк, которые будут возвращены запросом с данным предикатом.



